| True Value | Reconstructed/Predicted | |
|---|---|---|
| Premise | two women are embracing while holding to go packages. | two women are embracing while holding to go packages. |
| Hypothesis | two woman are holding packages. | two woman are holding packages. |
| Label | entailment | entailment |
Learning Galois-Structured Representations of Natural Language
December 8, 2025
Motivating Examples
- Premise: “Two women are embracing while holding to go packages”
- Hypothesis: “Two women are holding packages”
Relationship? → Entailment
- Premise: “Two children in blue jerseys… in a bathroom washing hands”
- Hypothesis: “Two kids at a ballgame wash their hands”
Relationship? → Contradiction
The Challenge
Central Problem: Representing sentence meaning for reasoning, composition, and interpretability
- Neural language models (e.g., BERT) produce powerful distributed representations
- But these embeddings lack explicit structure
- Struggle to capture semantic relationships like entailment
Our Approach
Learn a Galois connection between natural language and structured geometric abstractions
- Sentences → Boxes
- Semantic entailment ↔︎ Geometric containment
- Interpretable representations
What is a Galois Connection?
A Galois connection is a correspondence between two partially ordered domains
Natural Language Inference (NLI)
Task: Classify relationship between premise and hypothesis
- Entailment: Hypothesis logically follows from premise
- Premise box ⊇ Hypothesis box
- Contradiction: Hypothesis conflicts with premise
- Boxes are disjoint or violate containment ordering
- Neutral: No logical relationship
- Partial or no overlap
Dataset: SNLI Corpus
Stanford Natural Language Inference
- ~570,000 human-written English sentence pairs
- Three balanced classes: Entailment, Contradiction, Neutral
- Derived from image captions (Flickr 30k)
| Premise | Relation | Hypothesis |
|---|---|---|
| two women are embracing while holding to go packages. | entailment | two woman are holding packages. |
| two women are embracing while holding to go packages. | contradiction | the sisters are hugging goodbye while holding to go packages after just eating lunch. |
| two women are embracing while holding to go packages. | neutral | the men are fighting outside a deli. |
Model Architecture
Architecture Overview
- Abstraction Network (\(\alpha\)): BERT encoder → Box embeddings
- Maps sentences to axis-aligned hyperrectangles \([l, u]\)
- Concretization Network (\(\gamma\)): Transformer decoder
- Reconstructs natural language from boxes
- Box Lattice Operations: Geometric reasoning
- Volume, intersection, containment violations
- Geometric Feature Classifier: 3-layer feedforward
- 8 geometric features → Entailment/Contradiction/Neutral
Box Intersection Techniques
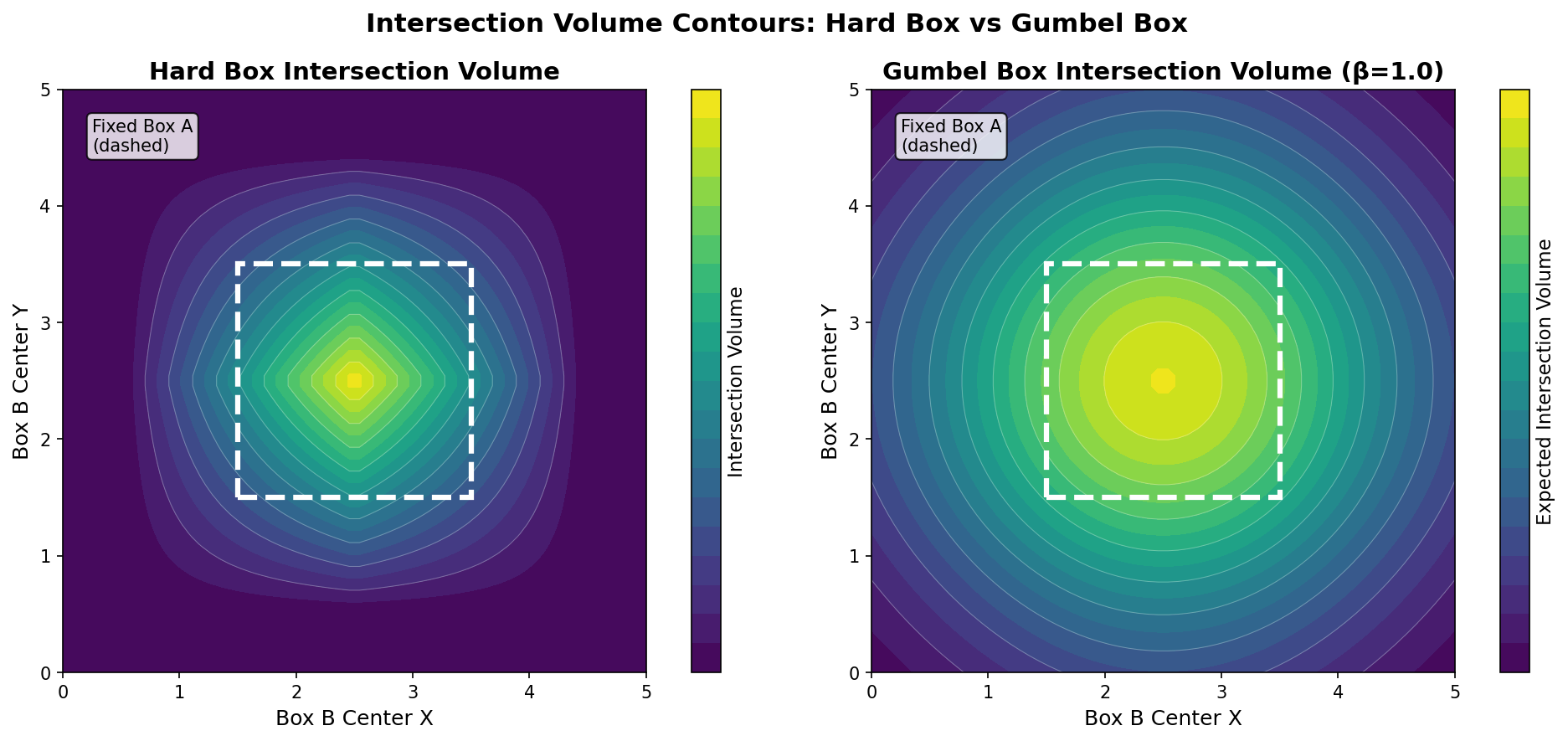
Hard vs. Probabilistic (Gumbel) intersection techniques
Soft [1] and Gumbel-smoothed [2] embeddings provide smoother gradients for optimization
Counterexample-Guided Abstraction Refinement
- Maintains buffer of misclassified examples
- Iteratively refines abstraction function
- Example: If model wrongly infers “Tom goes” ⊆ “Tom goes to jail”
- CEGAR detects counterexample
- Penalizes incorrect box containment
- Refines encoder to correct the relationship
Training Objective
Training aims to minimize the multi-component loss function:
\[ L = \lambda_{\text{recon}} L_{\text{recon}} + \lambda_{\text{Galois}} L_{\text{Galois}} + \lambda_{\text{task}} L_{\text{task}} + \lambda_{\text{CEGAR}} L_{\text{CEGAR}} + \lambda_{\text{reg}} L_{\text{reg}} \]
- \(L_{recon}\): Reconstruction quality
- \(L_{Galois}\): Geometric consistency
- \(L_{task}\): NLI classification
- \(L_{CEGAR}\): Refinement from counterexamples
- \(L_{reg}\): Prevent excessive box growth
Results
Overall Performance
- 80% validation accuracy on SNLI corpus
- F1 score: 80% across all classes
- Demonstrates viability of Galois connection framework
- Semantic entailment successfully learned as geometric containment
Per-Class Performance
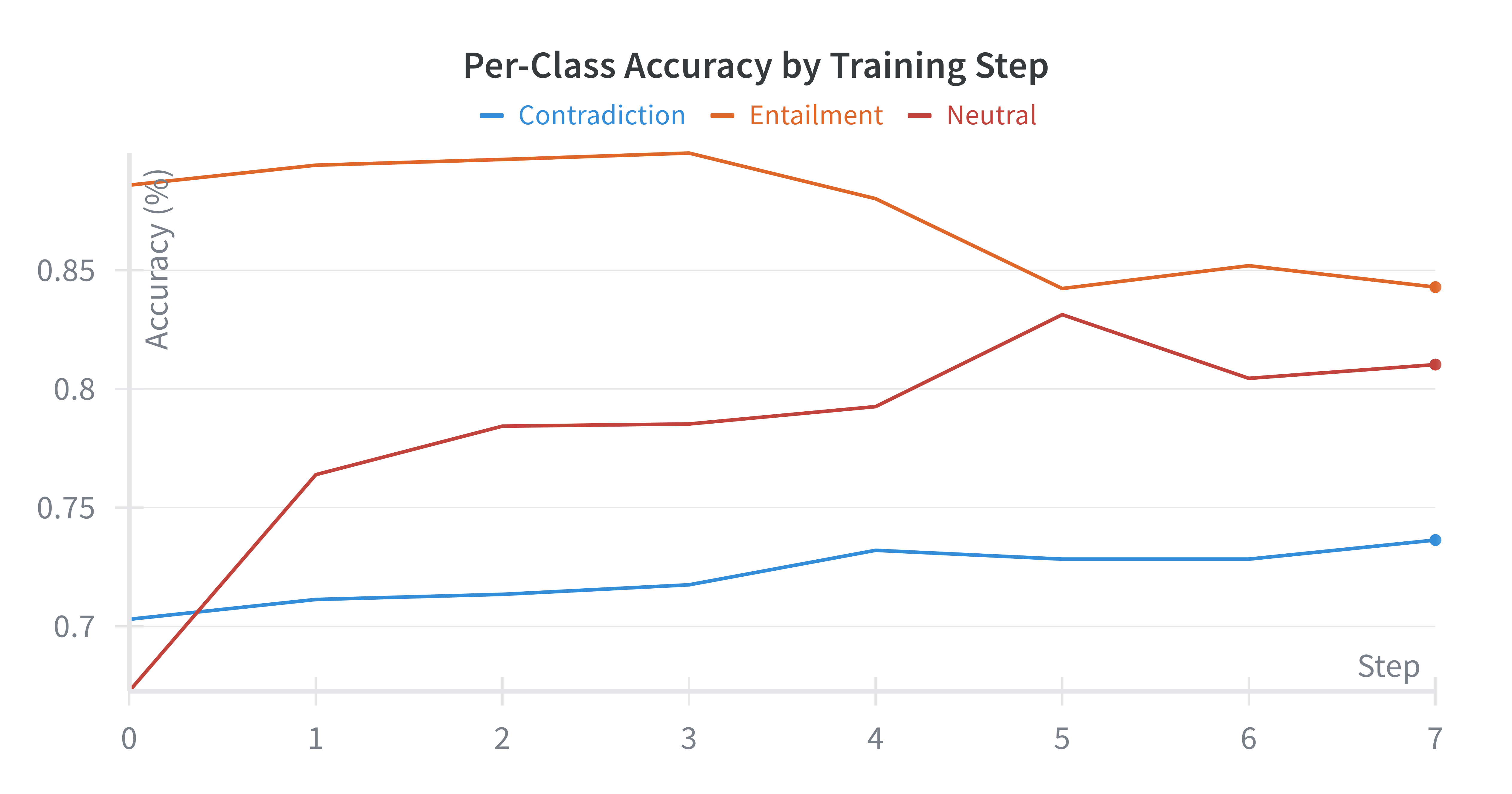
- Entailment learned first (straightforward geometric principle)
- Neutral and Contradiction improve steadily
- Challenge: Distinguishing subtle boundaries in shared geometric space
Reconstruction Quality
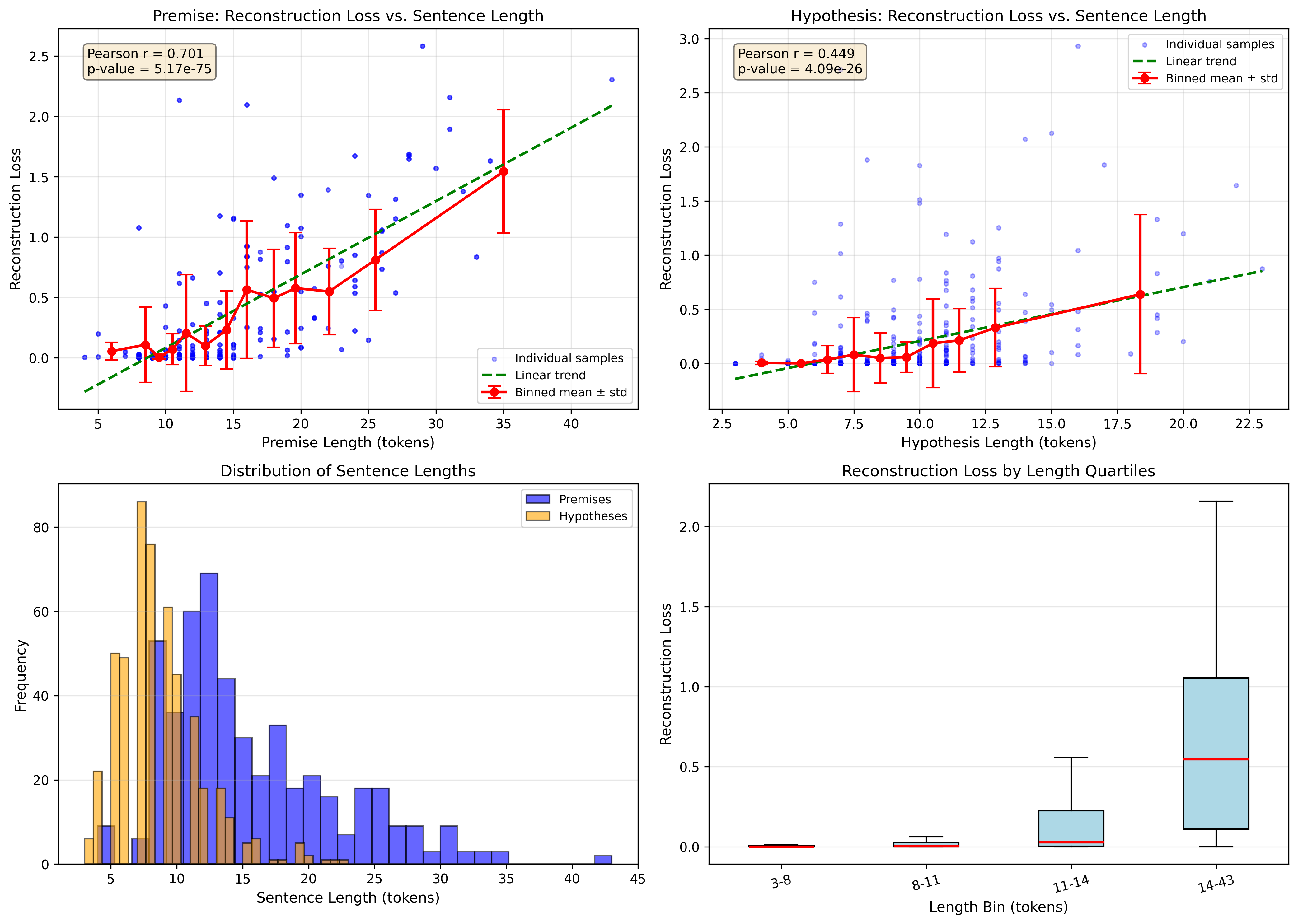
Strong correlation between phrase length and reconstruction loss (\(p < 0.001\))
- Shorter phrases → Effective compression and reconstruction
- Longer phrases → Information bottleneck in fixed-dimensional boxes
CEGAR Evaluation
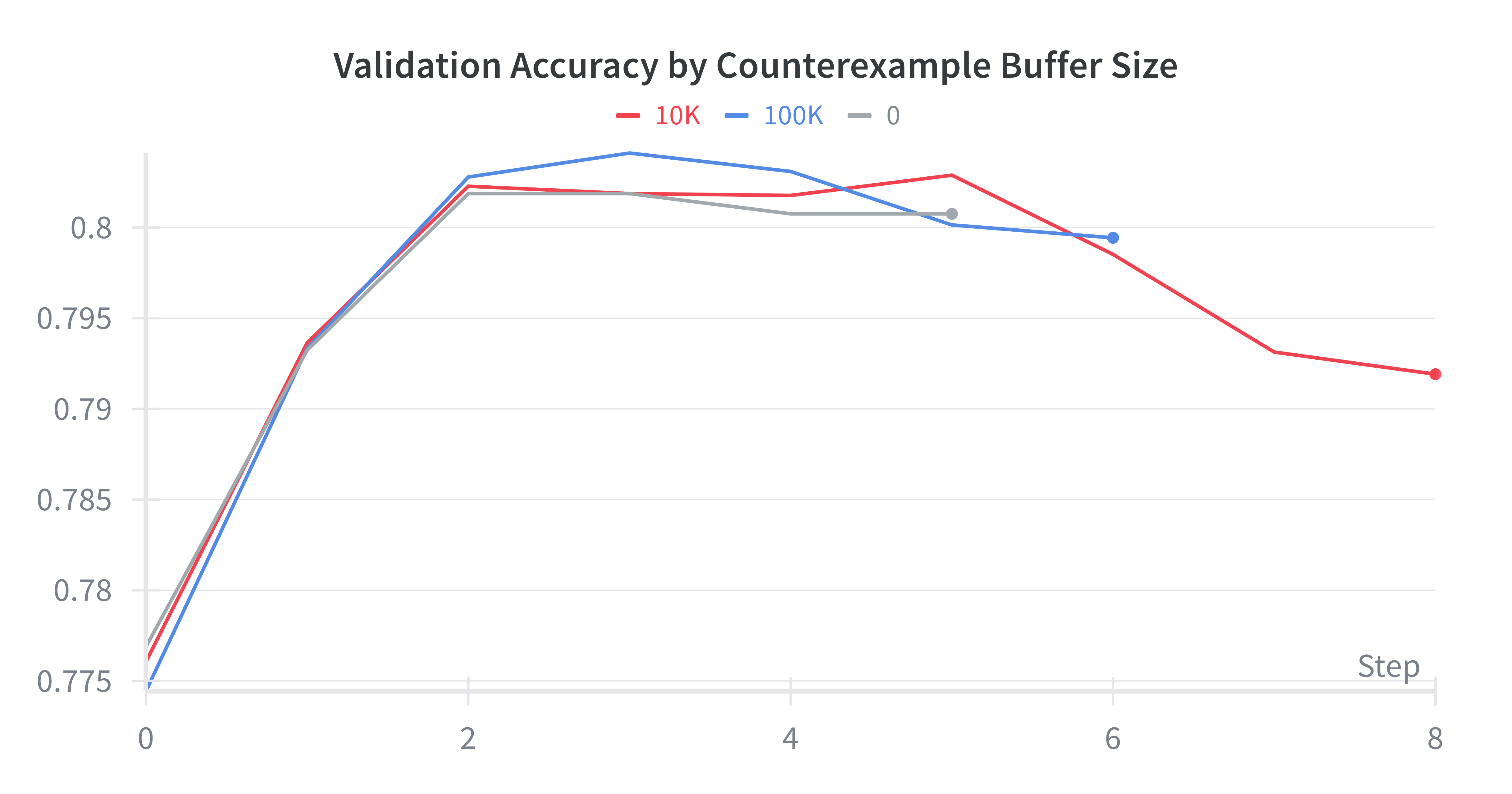
Unexpected Result: Buffer size had no significant impact on performance
- All configurations converged to ~80% accuracy
- Larger buffers introduced computational overhead
- Future work needed on alternative refinement strategies
Example: Entailment
Box representations successfully preserved semantic information
Example: Contradiction
| True Value | Reconstructed/Predicted | |
|---|---|---|
| Premise | two women are embracing while holding to go packages. | two women are embracing while holding to go packages. |
| Hypothesis | the sisters are hugging goodbye while holding to go packages after just eating lunch. | the sisters are hugging after hugging while holding up to go lunch break. |
| Label | contradiction | contradiction |
Specificity conflict identified, but longer hypothesis poorly reconstructed
Limitations
- Phrase Length Dependency
- Fixed-dimensional boxes → information bottleneck
- Longer phrases lose compositional complexity
- CEGAR Performance
- No measurable improvement from counterexample buffer
- Implementation vs. conceptual issues unclear
- Representational Capacity
- Questions about box lattices for complex semantics
Key Contributions
First end-to-end differentiable framework learning Galois connection for text
Structured latent space as complete lattice of boxes
- Interpretable, compositional abstractions
CEGAR mechanism for iterative semantic refinement
Integration of formal methods with deep learning
Future Directions
Multiple Datasets: MultiNLI, SICK for generalizability
Hyperparameter Optimization: Box dimensionality, loss weights, architecture choices
Baseline Comparisons: SBERT, fine-tuned LLMs
Interpretability Focus:
- Replace neural classifier with decision trees
- Visualization tools for high-dimensional box lattices
- Alignment with human semantic intuitions
Conclusions
- Abstract interpretation and representation learning can be combined for natural language understanding
- Semantic relationships can be captured as geometric containment in structured space
- Opens pathways for interpretable AI with formal guarantees
- Further opportunities for research in representational capacity and refinement mechanisms
Thank You
Questions?
Michael Thomas
Department of Computer Science
Furman University